We’re required to prove that the sum of opposite angles of a cyclic quadrilateral is 180°.
For this, we use Central Angle Theorem.
Central Angle Theorem
Angle subtended by an arc at the center is double the angle subtended by it on remaining part of the circle.

Proof:
Consider a Centre of the circle, Say O
Join Vertex A and C to center O
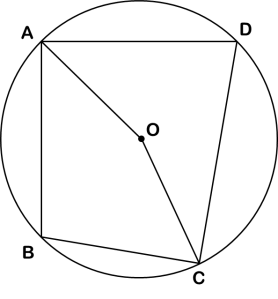
Consider minor ∠AOC
∠AOC=2∠D (Central Angle Theorem)

Let ∠AOC = x
Hence, ∠D becomes x/2

Major ∠AOC becomes 360-x
By Central Angle Theorem:
∠B = (360-x)/2
∠B = 180-(x/2)

Now, upon adding ∠B & ∠D, we get,
∠B + ∠D
=180 – (x/2) + (x/2)
=180°
That’s our answer!!

Leave a comment